Equation Of Conic Sections Polar Form
Equation Of Conic Sections Polar Form - Θ, where d is the distance to the directrix from the focus and e is the eccentricity. Web polar equations of conic sections: Aj speller · · sep 28 2014. Ellipse → a⋅ c > 0 and a ≠ c. To convert this cartesian equation to polar form, we will use the substitutions and. Planets orbiting the sun follow elliptical paths. Identify a conic in polar form. First, we should expand the expression: Graph the polar equations of conics. For a conic with a focus at the origin, if the directrix is x= ±p, x = ± p, where p p is a positive real number, and the eccentricity is a positive real number e, e, the conic has a polar equation.
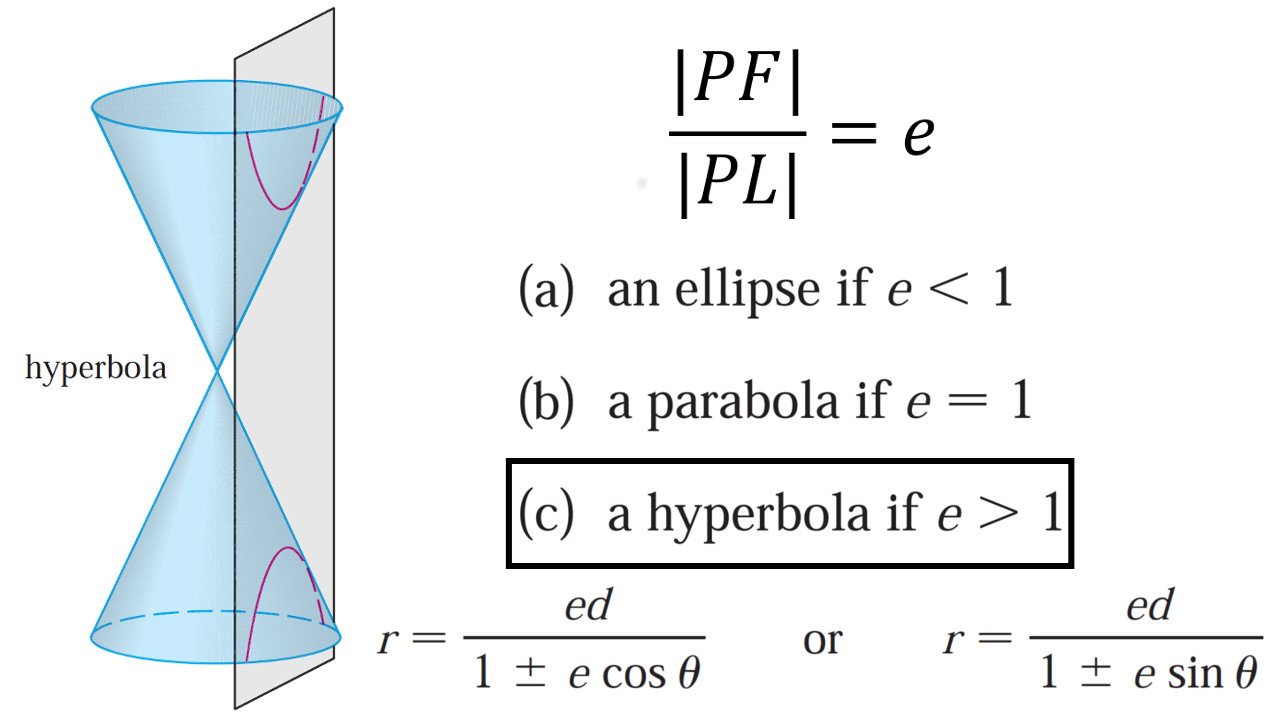
Web it explains how to identify the conic as an ellipse, parabola or hyperbola and how to determine the eccentricity and the equation of the directrix of the conic section. 9r2 = + 11 3r cos. Just as two (distinct) points determine a line, five points determine a conic. Web conic sections in polar coordinates. Web the general polar equation of conic sections. Define conics in terms of a focus and a directrix. Subtract 9 from both sides.
A locus of points is a set of points, each location of which is satisfied by some condition. Web the general polar equation of conic sections. The coefficients a and c are need to identify the conic sections without having to complete the square. Each conic section can be defined as a locus of points. Ax2 + bxy + cy2 + dx +ey + f = 0.
Web could someone show me how to find a polar form of this general equation of a conic section? Which conic section is represented by the rectangular equation? ( θ − θ 0), where the constant θ0 θ 0 depends on the direction of the directrix. This can be done by dividing both the numerator and the denominator of the fraction by the constant that appears in. Web polar equations of conics. Given the polar equation for a conic, identify the type of conic, the directrix, and the eccentricity.
Define conics in terms of a focus and a directrix. Web conic sections in polar coordinates. R=\frac {ep} {1\pm e\text { }\sin \text { }\theta } r = 1±e sin θep. A locus of points is a set of points, each location of which is satisfied by some condition. The polar equation of any conic section is r ( θ) = e d 1 − e sin.
A and c cannot be 0 when making this determination. R(θ) = ed 1 − e cos(θ − θ0), r ( θ) = e d 1 − e cos. A locus of points is a set of points, each location of which is satisfied by some condition. I have managed to determine this is an ellipse and write it in a canonical form with changed variables:
( Θ − Θ 0), Where The Constant Θ0 Θ 0 Depends On The Direction Of The Directrix.
Graph the polar equations of conics. Graph the polar equations of conics. Web the polar form of a conic. Web conic sections in polar coordinates.
X2 + Y2 − Xy + X = 4.
Web to work with a conic section written in polar form, first make the constant term in the denominator equal to 1. By the end of this section, you will be able to: Identifying a conic given the polar form. Web the polar equation for a conic.
Multiply The Numerator And Denominator By The Reciprocal Of The Constant In The Denominator To Rewrite The Equation In Standard Form.
Web then the polar equation for a conic takes one of the following two forms: 9.6 conic sections in polar coordinates. To convert this cartesian equation to polar form, we will use the substitutions and. Define conics in terms of a focus and a directrix.
Multiply The Numerator And Denominator By The Reciprocal Of The Constant In The Denominator To Rewrite The Equation In Standard Form.
Web it explains how to identify the conic as an ellipse, parabola or hyperbola and how to determine the eccentricity and the equation of the directrix of the conic section. R = when r = , the directrix is horizontal and p units above the pole; Given the polar equation for a conic, identify the type of conic, the directrix, and the eccentricity. For each of the following equations, identify the conic with focus at the origin, the directrix, and the eccentricity.